Исследование конфигураций
К «бильярдным столам» относятся периодические конфигурации, в которых «ротор» (изменяющаяся часть) расположена внутри «статора» (неизменная часть). Часто можно расположить рядом несколько бильярдных столов или даже заполнить ими всю плоскость. Например, если размножить вертушку, получается следующая конфигурация:

Аналогично можно поступить и с осциллятором Герца.
Следующая конфигурация через четыре хода превращается в размноженный скребок.

Оказывается, что скребок можно немного укоротить.

А еще у каждой из перечисленных конфигураций есть устойчивые модификации.
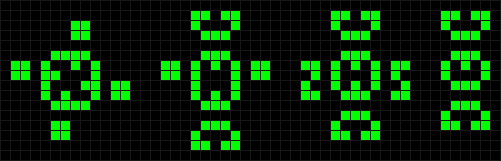
Разумеется, ими тоже можно заполнить плоскость.
Выстраивать в ряд можно не только относительно независимые объекты вроде бильярдных столов, но и интенсивно взаимодействующие части. Например, если взять не два челнока, а три, вместо обычного планерного ружья получится двустволка:

Этим методом легко получить ружья с произвольным количеством «стволов».
Как известно, пентадекатлон способен поглощать планеры, выпущенные ружьём.

Оказывается, роль поглотителя может сыграть и само планерное ружьё! Вот целая перестрелка между двумя ружьями:

НЛО через два хода превращается в два разлетающихся планера.

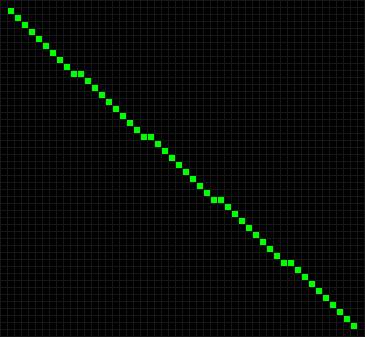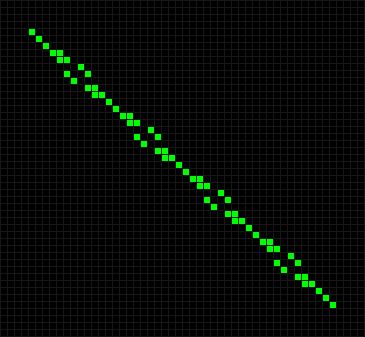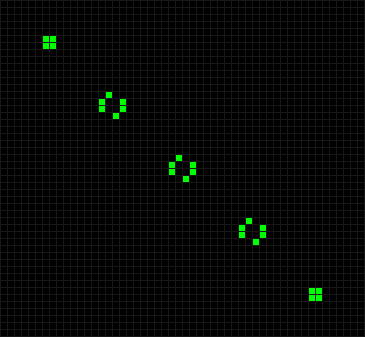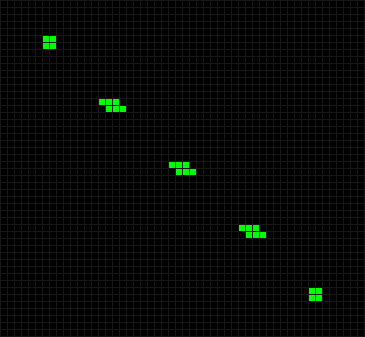
Интересные результаты обнаруживаются при небольшой модификации диагональной линии. Например, если её разбить на звенья длиной 5 и 6 фишек и сместить каждое звено относительно предыдущего на одну фишку, то на восьмом ходу такая линия распадается на разлетающиеся планеры.
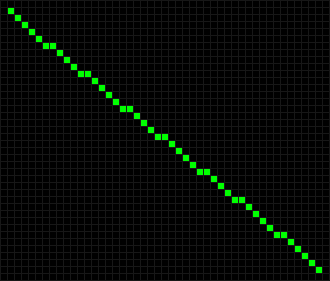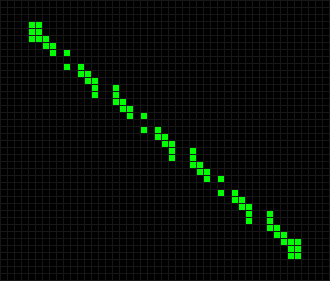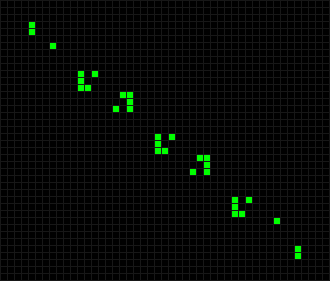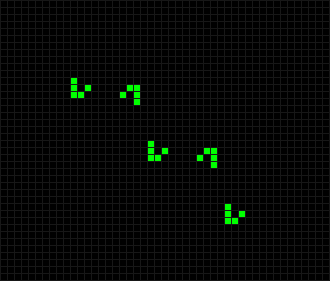
А если диагональ разбивать на звенья длиной 10 фишек, то на шестом ходу линия превратится в жабы.