Игра «Жизнь» (обзор Гарднера)

Книга Мартина Гарднера «Математические досуги» вышла в 1972 году. Её последняя глава посвящена игре «Жизнь». Хотя с тех пор в «Жизни» было сделано много интересных открытий, этот обзор по-прежнему будет весьма полезен для первого знакомства. Здесь представлено исправленное, дополненное и адаптированное для интернета издание этого обзора.

Что наша «Жизнь»? Игра!

Игру «Жизнь» придумал американский математик Джон Хортон Конуэй (хотя его научные интересы вполне серьезны, например, теория групп и теория чисел). Для этой игры вам не понадобится партнер — в неё можно играть одному. Возникающие в её процессе ситуации очень похожи на реальные процессы, происходящие при зарождении, развитии и гибели колонии живых организмов. По этой причине «Жизнь» можно отнести к быстро развивающейся в наши дни категории игр, имитирующих процессы, происходящие в живой природе.

Для игры «Жизнь» вам может понадобиться большая доска, разграфлённая на клетки, и много плоских фишек двух цветов (например, просто несколько наборов обычных шашек небольшого диаметра или пуговиц двух цветов). Можно рисовать ходы и на бумаге. Но значительно проще воспользоваться программами, моделирующими эту игру на компьютере.

Основная идея «Жизни» состоит в том, чтобы, начав с какого-нибудь простого расположения фишек (организмов), расставленных по одной в клетке, проследить за эволюцией исходной позиции под действием «генетических законов» Конуэя, которые управляют рождением, гибелью и выживанием фишек. Конуэй тщательно подбирал свои правила, и долго проверял их «на практике», добиваясь, чтобы они по возможности удовлетворяли трём условиям:

1. Не должно быть ни одной исходной конфигурации, для которой существовало бы простое доказательство возможности неограниченного роста популяции.

2. В то же время должны существовать такие начальные конфигурации, которые заведомо обладают способностью беспредельно развиваться.

3. Должны существовать простые начальные конфигурации, которые в течение значительного промежутка времени растут, претерпевают разнообразные изменения и заканчивают свою эволюцию одним из следующих трёх способов: полностью исчезают (либо из-за перенаселённости, то есть слишком большой плотности фишек, либо наоборот, из-за разрежённости фишек, образующих конфигурацию), переходят в устойчивую конфигурацию и перестают изменяться вообще или же, наконец, выходят на колебательный режим, то есть бесконечный цикл превращений с определенным периодом.

Короче говоря, правила должны быть такими, чтобы поведение популяции было непредсказуемым.

Генетические законы Конуэя удивительно просты. Прежде, чем мы их сформулируем, обратим внимание на то, что каждую клетку доски (доска считается бесконечной), окружают восемь соседних клеток: четыре имеют с ней общие стороны, четыре другие — общие вершины. Правила игры (генетические законы) сводятся к следующему:

1. Выживание. Каждая фишка, имеющая вокруг себя две или три соседние фишки, выживает и переходит в следующее поколение.

2. Гибель. Каждая фишка, у которой больше трёх соседей, погибает, то есть снимается с доски из-за перенаселённости. Каждая фишка, вокруг которой свободны все соседние клетки или же занята всего одна клетка, погибает от одиночества.

3. Рождение. Если число фишек, с которыми граничат какая-нибудь пустая клетка, в точности равно трём (не больше и не меньше), то на этой клетке происходит рождение нового «организма», то есть следующим ходом на неё ставится одна фишка.

Важно понять, что рождение и гибель всех «организмов» происходит одновременно. Вместе взятые, они образуют одно поколение или, как мы будем говорить, один ход в эволюции начальной конфигурации. Ходы Конуэй рекомендует делать следующим образом:

1. начать с конфигурации, целиком состоящей из черных фишек;
2. определить, какие фишки должны погибнуть, и положить на каждую из обреченных фишек по одной черной фишке;
3. найти все свободные клетки, на которых должны произойти акты рождения, и на каждую из них поставить по одной фишке белого цвета;
4. выполнив все эти указания, ещё раз внимательно проверить, не сделано ли каких-либо ошибок, затем снять с доски все погибшие фишки (то есть столбики из двух фишек), а всех новорожденных (белые фишки) заменить черными фишками.

Проделав все операции, вытекающие из генетических законов, вы получите первое поколение в эволюции первоначальной конфигурации. Аналогичным образом получаются и все последующие поколения. Теперь уже ясно, для чего нужны фишки двух цветов: поскольку рождение и гибель «организмов» происходит одновременно, новорожденные (например, белые) фишки никак не влияют на гибель и рождение остальных (чёрных) фишек, и поэтому, проверяя новую конфигурацию, необходимо уметь отличать их от фишек, перешедших из предыдущего поколения. Допустить ошибку, в особенности, если вы играете впервые, очень легко. Со временем вы будете делать всё меньше и меньше ошибок, однако даже опытные игроки должны очень внимательно проверять каждое новое поколение перед тем, как снимать с доски погибшие фишки и заменять чёрными фишками новорожденные белые.

Начав игру, вы сразу заметите, что многие популяции непрестанно претерпевают необычные, нередко очень красивые и всегда неожиданные изменения. Иногда первоначальная колония организмов постепенно вымирает, то есть все фишки исчезают, однако произойти это может не сразу, а лишь после того, как сменится очень много поколений. В большинстве своем исходные конфигурации либо переходят в устойчивые (любители спокойной жизни), и перестают изменяться, либо навсегда переходят в колебательный режим. Конфигурации, не обладавшие в начале игры симметрией, обнаруживают тенденцию к переходу в симметричные формы. Обретённые свойства симметрии в процессе дальнейшей эволюции не утрачиваются (генетические законы не зависят от расположения фишек на доске), симметрия конфигурации может лишь обогащаться.

Конуэй высказал гипотезу, согласно которой не существует ни одной начальной конфигурации, способной беспредельно расти. Иначе говоря, любая конфигурация, состоящая из конечного числа фишек, не может перейти в конфигурацию, в которой число фишек превосходило бы некий конечный верхний предел. Это, наверное, одна из самых глубоких и самых сложных задач, возникающих в «Жизни». Когда описание игры появилось в октябрьском номере журнала Scientific American за 1970 год, Конуэй предлагал премию тому, кто до конца года первым докажет или опровергнет его гипотезу.

Теперь посмотрим, что происходит с некоторыми простыми конфигурациями.

Одна фишка, а также любая пара фишек, где бы они ни стояли, очевидно, погибают после первого же хода.

Исходная конфигурация из трёх фишек (будем называть её триплетом), как правило, погибает. Выживает триплет лишь в том случае, если, по крайней мере, одна фишка граничит с двумя занятыми клетками. Пять триплетов, не погибающих на первом же ходу, изображены на рисунке. (Как расположены триплеты на плоскости — прямо, «вверх ногами» или косо, не существенно.)

Первые три конфигурации на втором ходу погибают. Относительно третьей конфигурации заметим, что любой диагональный ряд фишек, каким бы длинным он ни был, с каждым ходом теряет стоящие на его концах фишки и, в конце концов, совсем исчезает. Скорость, с которой шахматный король перемещается по доске в любом направлении, Конуэй называет скоростью света. (Причины этого станут понятны в дальнейшем.) Пользуясь этой терминологией, можно сказать, что диагональный ряд фишек распадается с концов со скоростью света.

Четвёртая конфигурация на втором ходу переходит в устойчивую конфигурацию — блок размером 2×2. Пятая конфигурация служит простейшим примером так называемых флип-флопов (кувыркающихся конфигураций, возвращающихся в исходное состояние через каждые два хода). Она попеременно превращается то в вертикальный, то в горизонтальный ряд из трёх фишек. Конуэй называет этот триплет мигалкой.

Рассмотрим эволюцию пяти тетрамино (четыре клетки, из которых состоит элемент тетрамино, связаны между собой ходом ладьи).

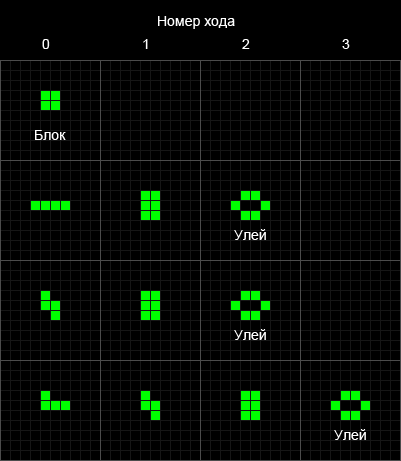
Как мы уже видели, первый квадрат относится к категории любителей спокойной жизни. Вторая и третья конфигурация после второго хода переходит в устойчивую конфигурацию, называемую ульем. Ульи в игре возникают часто. Четвёртое тетрамино также превращается в улей, но на третьем ходу.

Особый интерес вызывает ещё одно тетрамино, которое после девятого хода распадается на четыре отдельные мигалки (вся конфигурация носит название навигационные огни).

Навигационные огни относятся к разряду флип-флопов и возникают довольно часто.

Двенадцать наиболее часто встречающихся конфигураций из числа любителей спокойной жизни (то есть устойчивых конфигураций) приведены на этом рисунке.

Пасека является устойчивой конфигурацией из четырёх ульев, в которую после 14 ходов переходит горизонтальный ряд из 7 фишек. Квадрат размером 5×5 после первого же хода переходит в конфигурацию, которая возникает лишь на четвёртом этапе эволюции семиклеточного ряда. Поэтому квадрат 5×5 становится пасекой после 11 ходов.

Вы можете самостоятельно поэкспериментировать с двенадцатью фигурами пентамино (фигуры, состоящие из пяти клеток, связанных между собой так, что их можно обойти ходом ладьи) и посмотреть, во что они превращаются. Оказывается, что пять из них на пятом ходу погибают, две быстро переходят в устойчивые конфигурации из семи клеток, а четыре после небольшого числа ходов превращаются в навигационные огни.

Единственным исключением является элемент пентамино, имеющий форму буквы r, превращения которого заканчиваются не столь быстро (превращения конфигурации считаются исчерпанными, ели та исчезает, переходит в устойчивую конфигурацию или начинает периодически пульсировать).

Конуэй проследил развитие r-образного пентамино вплоть до четыреста шестидесятого хода, после которого конфигурация распалась на множество планеров. Конуэй пишет, что «от фигуры осталось множество мертвых (не изменяющихся) обломков и лишь несколько областей, в которых всё ещё теплилась жизнь, поэтому отнюдь не очевидно, что процесс эволюции должен происходить бесконечно долго. После сорока восьми ходов r-образное пентамино превратилось в конфигурацию, левая часть которой состоит из семи фишек, а правая — из фишек, заполняющих две симметричные области. Если бы левой части не было, то эти области развивались бы в пасеку с четырьмя ульями и навигационные огни. Возмущение, вносимое левой частью, приводит к тому, что пасека быстро вгрызается в навигационные огни и образующие их четыре мигалки гаснут одна за другой, оставляя после себя на доске „нечто бесформенное“».

Изучая эволюцию долгожителей наподобие r-пентамино, Конуэй иногда пользуется вычислительной машиной, устройство которой позволяет выводить выходные данные на экран и таким образом наблюдать все изменения, происходящие на игровом поле. Без программы, которую написали М. Дж. Т. Гай и С. Р. Бурн, многие особенности игры были бы обнаружены лишь с большим трудом. Эволюция r-пентамино была прослежена до конца с помощью компьютерных вычислений. Она завершается лишь после тысяча сто третьего хода. Шесть возникших на доске планеров удаляются от центра на всё большее и большее расстояние (находятся за пределами рисунка), и, в конце концов, вокруг бывшего пентамино (показано красным цветом) остаются четыре мигалки, один корабль, одна лодка, один каравай, четыре улья и восемь блоков.

В качестве простых упражнений проследите до конца эволюцию двух фигур: латинского креста и буквы „Н“.

Если перекладину в букве „Н“ поднять на одну клетку вверх, чтобы получились ворота (или, как называет эту конфигурацию Конуэй, прописная буква «пи»), то произойдут совершенно неожиданные изменения. В противоположность букве „Н“, эволюция которой заканчивается быстро, ворота оказываются весьма долгоживущей конфигурацией. Лишь после 173 ходов она распадается на 5 мигалок, 6 блоков и 2 пруда.

Также легко проследить эволюцию вертушки, бакена, часов и жабы.

Последние три конфигурации периодически воспроизводят себя (период равен двум ходам; ранее мы называли такие конфигурации флип-флопами). По словам самого Конуэя, жаба дышит, часы тикают, бакен зажигается, и в каждом случае период равен двум. Внутренняя часть вертушки с каждым следующим ходом поворачивается на 90°, а все внешние фишки остаются на своих местах. Подобные периодические конфигурации Конуэй называет бильярдными столами, чтобы отличать их от истинно периодических конфигураций, таких, как, например, жаба, часы и бакен.

Конуэй проследил эволюцию всех элементов гексамино и всех элементов гептамино, за исключением семи.

Одним из самых замечательных открытий Конуэя следует считать конфигурацию из 5 фишек — планер.

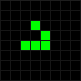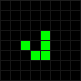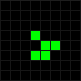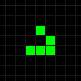
После второго хода планер немного сдвигается и отражается относительно диагонали. В геометрии такой тип симметрии называется скользящей симметрией, отсюда и название фигуры (По-английски планер называется glider, от glide — скользить. — Прим. перев.). В результате двух последующих ходов планер «выходит из пике», ложится на прежний курс и сдвигается на одну клетку вправо и на одну клетку вниз относительно начальной позиции.

Выше уже писалось, что скорость шахматного короля в «Жизни» принято называть скоростью света. Выбор Конуэя пал именно на этот термин из-за того, что в изобретённой им игре большие скорости просто не достигаются. Ни одна конфигурация не воспроизводит себя достаточно быстро, чтобы двигаться с такой скоростью. Конуэй доказал, что максимальная скорость по диагонали составляет одну четверть скорости света. Поскольку планер переходит сам в себя после четырех ходов и при этом опускается на одну клетку по диагонали, то говорят, что он скользит по полю со скоростью, равной одной четвёртой скорости света.

Конуэй также показал, что скорость любой конечной фигуры, перемещающейся по вертикали или по горизонтали на свободные клетки, не может превышать половину скорости света. Конуэю известны и другие движущиеся конфигурации, кроме планера, которые он называет космическими кораблями. На рисунке показаны три космических корабля. Все они передвигаются горизонтально слева направо со скоростью, равной половине скорости света. В полёте из них вылетают «искры», которые тут же гаснут при дальнейшем движении кораблей.

Одиночные космические корабли без эскорта не могут занимать в длину больше шести клеток, в противном случае на доске начинают появляться различные мелкие фигуры, препятствующие движению корабля. Конуэй обнаружил, что более длинным кораблям (которые он назвал сверхтяжёлыми) необходим эскорт из двух или большего числа кораблей меньших размеров. Корабли эскорта не дают возникать препятствиям на пути сверхтяжёлого корабля. На рисунке изображён самый большой космический корабль, для которого достаточно двух эскортирующих кораблей меньшего размера. Для более длинных кораблей необходима целая флотилия эскортирующих кораблей. Конуэй вычислил, что корабль длиной в сто клеток требует эскорта, состоящего из тридцати двух кораблей.

Восьмёрка — это периодически восстанавливающая себя конфигурация, открытие которой принадлежит Нортону. Она не только по форме напоминает восьмёрку, но и имеет период, равный восьми.

Следующая конфигурация называется пульсар СР 48-56-72. Она также периодически восстанавливает себя через каждые три хода. Начальное состояние пульсара образовано 48 фишками; на втором этапе число фишек возрастает до 56, а на третьем — до 72, после чего пульсар снова возвращается в исходное состояние, а число фишек понижается до 48.

Пульсар образуется после 32 ходов из элемента гептамино, имеющего вид растянутой буквы П: горизонтального ряда из пяти фишек, у которого под первой и последней фишкой располагается ещё по одной фишке.

Конуэй исследовал эволюцию всех горизонтальных рядов из n фишек вплоть до n = 20. Мы уже знаем, что происходит при n < 5. Пятиклеточный ряд переходит в навигационные огни, шестиклеточный исчезает, из семиклеточного получается пасека, из восьмиклеточного — четыре улья и четыре блока, девятиклеточный ряд превращается в два комплекта навигационных огней, а ряд, состоящий из десяти фишек, переходит в пентадекатлон — периодически воспроизводящую себя конфигурацию с периодом, равным пятнадцати. Ряд из одиннадцати фишек эволюционирует, превращаясь в две мигалки; двенадцатиклеточный ряд переходит в два улья, тринадцатиклеточный — в две мигалки. Если ряд состоит из 14 или 15 фишек, то он полностью исчезает, а если фишек 16, то получается большой набор навигационных огней, состоящий из восьми мигалок. Эволюция семнадцатиклеточного ряда заканчивается четырьмя блоками; ряды, состоящие из 18 или 19 фишек, полностью исчезают с доски, а эволюция двадцатиклеточного ряда завершается двумя блоками.

Конуэй также исследовал эволюцию рядов, образованных пятиклеточными группами, отделенными друг от друга одной свободной клеткой. Ряд 5-5 после двадцать первого хода превращается в пульсар СР 48-56-72. Ряд 5-5-5 переходит в четыре блока и четыре мигалки; в результате эволюции ряда 5-5-5-5 получаются четыре пасеки и четыре мигалки; ряд 5-5-5-5-5 заканчивает свои превращения «эффектно разбросанными» по доске восемью планерами и восемью мигалками. Затем планеры попарно сталкиваются и, разрушаясь, превращаются в восемь блоков. Ряд, состоящий из шести групп по пяти клеток в каждой (5-5-5-5-5-5), превращается в четыре мигалки, а эволюция следующего ряда 5-5-5-5-5-5-5, по мнению Конуэя, представляет «замечательное зрелище, если наблюдать её на экране вычислительной машины». Конфигурация после 323 ходов стабилизируется, превратившись в четыре навигационных огня, восемь мигалок, восемь караваев, восемь ульев и четыре блока, то есть в конфигурацию, насчитывающую 192 фишки.

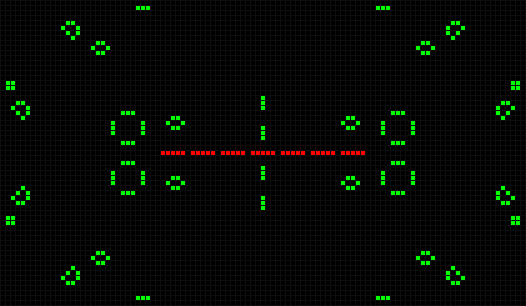
Поскольку симметрия начальной конфигурации не утрачивается при её последующей эволюции, расположение фишек сохраняет вертикальную и горизонтальную оси симметрии, которыми обладала начальная конфигурация. Число фишек достигает максимума (492 фишки) в 283 поколении.

Стоит заметить, что ряды типа n-n-n-... интересны лишь тогда, когда n равно по крайней мере 5, поскольку при меньших значениях n группы из n фишек не взаимодействуют друг с другом. Ряды 1-1-1-... и 2-2-2-... сразу же исчезают. Ряд 3-3-3-... состоит из одних лишь мигалок, а ряд 4-4-4-... на втором ходу переходит в устойчивый ряд ульев.

В ноябре 1970 года Конуэю пришлось выдать обещанную премию. Группа математиков из Массачусетского технологического института сумела построить ружьё, стреляющее планерами! Каждые 30 ходов из ружья вылетает планер. С появлением нового планера число фишек на доске увеличивается на 5, следовательно, происходит неограниченный рост популяции.

Планерное ружьё позволило его создателям совершить и много других замечательных открытий. Например, на рисунке показано столкновение 13 планеров. Рассыпавшись на части, они превращаются... в планерное ружьё!

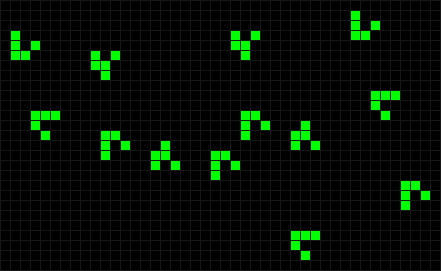
Та же группа исследователей обнаружила пентадекатлон — конфигурацию, способную «поглотить» сталкивающийся с ней планер.

Пентадекатлон может также отражать планер, изменяя курс последнего на 180°. Расположив друг против друга два пентадекатлона, можно провести между ними «теннисный матч»: они будут перекидывать планер, как мяч (период конфигурации на рисунке равен 60, показано каждое четвертое поколение).

Совершенно неожиданные результаты возникают при рассмотрении пересекающихся потоков планеров: возникающие конфигурации могут быть самыми причудливыми и в свою очередь испускать планеры. Иногда конфигурация, образующаяся при пересечении потоков планеров, начинает расти и, расширяясь, поглощает все ружья. В других случаях осколки, вылетающие из области, в которой происходит пересечение потоков, могут вывести из строя одно или несколько ружей. Последнее достижение группы математиков из Массачусетского технологического института, убедительно свидетельствующее об их виртуозности, — хитроумная комбинация нескольких ружей. В пересечении создаваемых ею потоков планеров возникает целый завод космических кораблей легчайшего типа, а каждые 300 ходов происходит даже запуск одного корабля!

Было открыто много других периодически воспроизводящихся конфигураций. Одна из них, получившая название палка, имеет период 2 (ранее мы называли «кувыркающиеся» конфигурации такого типа флип-флопами). Её можно как угодно растягивать. Каждое из двух её состояний переходит в другое при отражении.

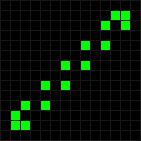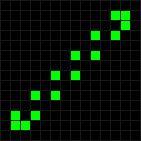
Другая была ещё раньше открыта Конуэем — это так называемый осциллятор Герца. После каждых четырёх ходов внутренняя точка перемещается к противоположной стороне рамки, в результате чего вся фигура «осциллирует» с периодом 8.

Третья конфигурация называется тумблер, потому что каждые 7 ходов у неё меняются местами верх и низ (она «переключается»).

Чеширского кота открыл К. Р. Топкинс из Калифорнии. После шести ходов от кота остается лишь «улыбка», а «морда» совершенно исчезает. Следующим ходом «улыбка» тоже уничтожается, и лишь неизменный блок — отпечаток кошачьей лапы — напоминает о том, что некогда на этом месте находился кот.

Жнейка движется снизу вверх по бесконечной диагонали со скоростью света, осциллируя с периодом, равным 4, и вдоль всего пути оставляет за собой устойчивые фигуры, символизирующие снопы. «К сожалению, — пишет изобретатель жнейки, — мне не удалось придумать «сеятеля» — движущуюся фигуру, которая могла бы засевать поле с той же скоростью, с которой жнейка его убирает».

Вейнрайт, изобретатель планерного ружья, является автором многих любопытных исследований. Разместив случайным образом 4800 фишек в ячейках квадрата размером 120×120 (с плотностью фишек, равной 1/3), он проследил их эволюцию на протяжении 450 поколений. Плотность этого первообразного студня, как его называет Вейнрайт, сильно уменьшилась и стала равняться всего лишь 1/6. Исчезнут ли все фишки в конце концов или же будут, как утверждает Вейнрайт, продолжать просачиваться из поколения в поколение с некоторой минимальной постоянной плотностью — ответ на этот вопрос пока не известен. На протяжении 450 поколений удалось проследить появление 42 «короткоживущих» планеров.

Вейнрайту удалось обнаружить 14 конфигураций, которые после первого хода превращаются в один или несколько планеров. Например, из первой фигуры, показанной на рисунке ниже, получается один планер. Буква „Z“ (вторая конфигурация) после 12 ходов превращается в 2 планера, которые движутся в противоположных направлениях. Если два планера следуют наперерез друг другу (третья конфигурация), то после четвёртого хода все фишки с доски исчезают. Если два лёгких космических корабля движутся опасным курсом, ведущим к столкновению (последняя фигура), то после седьмого хода доска оказывается абсолютно пустой, как и в случае столкновения двух планеров.

Вейнрайт, кроме того, экспериментировал с разными бесконечными полями, заполняя их правильными устойчивыми фигурами. Такие конфигурации он назвал агарами. (Агар — продукт, получаемый из некоторых морских водорослей. Хорошо растворяется в горячей воде, образуя после охлаждения плотный студень. Применяется при разведении бактерий в качестве твердой среды для выращивания микроорганизмов.)

Если, например, в агар, изображённый ниже, поместить один-единственный «вирус» (то есть одну фишку), причём так, чтобы он касался вершин четырёх блоков, то агар уничтожит вирус, а через два хода восстановит свой прежний вид. Если же вирус поместить в клетку так, как показано на рисунке красным цветом, то начнётся неизбежное разрушение агара.

Вирус постепенно поглотит внутри агара все активные участки, оставив на поле пустую двусторонне симметричную область (грубо говоря, восьмиугольной формы). Её граница непрерывно расширяется во все стороны со скоростью света, и не исключено, что это расширение будет происходить бесконечно долго.

• ↑ The Game of Life
• ←
• → Клеточные автоматы (обзор Гарднера)

© Роман Парпалак, 2011. Сайт работает на движке S2.